Lars' Blog

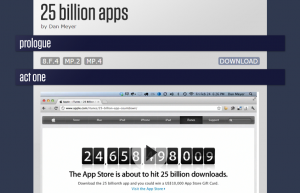
As a class, we are responding to the math task “25 Billion Apps” from the site

Our source website.

I believe that we should start bombarding the App Store with downloads on Thursday, March 1 at 2:47:44 PM LA Pacific Standard Time. I reached this conclusion by first taking the number of downloads at 6:27, 6:28, and 6:29 on Friday, February 24. I found the difference between 6:28 and 6:27, and 6:29 and 6:28. I took the average of the two numbers, to get an average rate of change of 34,631.5 downloads per minute. Then, I found the difference between 25 billion and the number of downloads at 6:29. Next, I divided the difference by the average rate of change, discovering how many minutes had passed. I then divided this number by 60, finding the number of hours that had passed. I then divided that number by 24, finding how many days had passed. In the end, I had 6 days, 20 hours, and 18 minutes having passed, and added them on to 6:29 PM February 24, getting my final answer.

I enjoy being able to retake tests and use the computers. However, I would like to do blog posts slightly less. The class is very fun and hands-on.

I can add, subtract, multiply, and divide negative numbers. I have a sufficient understanding of the concept and got a 100% on the assessment on the subject. I can perform the distributive property, and can combine like terms using the distributive property. I am clear on how the distributive property works and can then combine like terms. I have gotten a 100% on the test. I can evaluate positive, zero, and negative exponents, and can simplify expressions using exponents. I feel that I understand exponents.

I would give my self an A in this class. I have a clear understanding of the topics we have learned, and have done well on the assessments.

Hello! The past few weeks we have been learning about rules and properties of exponents.

When multiplying exponents with the same bases, you simply add the exponents. Here is an example.

x^7 * x^5 = x*x*x*x*x*x*x * x*x*x*x*x = x^12

Notice how the multiplication symbol connects the string of numbers from x^7 to x^5.

When dividing exponents, subtract the exponents in the denominator from the exponent in the numerator.

For example:  x^9/x^3 = x/x * x/x * x/x * x^6 = x^6

Any number over itself is 1, so that leaves us with x^6, because the Identity Property states that any number multiplied by 1 is the same number.

When taking an exponent to another exponent, multiply the exponents.

(x^7)^9=x^63

When you have a negative exponent, multiply by the reciprocal.

8^-4=1/8 * 1/8 * 1/8 * 1/8 =1/4096

Hello! Today I’m going to work you, the audience, through finding the square root of 190 to the nearest tenth.

First of all, 190 is between two perfect squares. In this case, these are 169 and 196.

13*13=169 and 14*14=196.

Because we know that our square root is more than 13, but not yet 14, the whole number in our root needs to be 13.

To begin to narrow down the decimals, let’s find the number halfway between the two squares.

196-169=27 and 27/2=13.5          169+13.5=182.5

190 is greater than 182.5, so that means we can rule out 13.1 through 13.4. Now, let’s find the halfway point again.

196-182.5=13.5 and 13.5/2=6.75       182.5+6.75= 189.25, meaning that the square root of 189.25 is approximately 13.75.

This is still less than 190, but it’s very close, so we can pretty safely assume that the square root of 190 is approximately 13.8.

If we put this in the calculator, the square root of 190 is about 13.784, so we were correct.

I like my blog theme, but I really wish it showed the pages I publish.

This week we took our first math test. It was on adding, subtracting, multiplying, and dividing negative numbers and combining like terms. When adding a negative number, keep in mind that it’s pretty much the same as subtracting a positive. When subtracting a negative,  it’s the same as adding a positive. When multiplying, multiply the two numbers together and count the amount of negative factors in the expression. If the number of negative factors is odd, the answer is negative. If the number is even, the number is positive.

Here’s an example.

4*-7=-28

-3*-5=15

I figured out how to post! >:)

This is my math class blog.